Phred Adjusted Maximum Likelihood Decoding
Phred Adjusted Maximum Likelihood Decoding, abbreviated PAMLD, is a closed class decoding algorithm that directly computes the decoding likelihood from the base calling error probabilities provided by the sequencing platform and a set of priors for noise and the potential barcode sequences. As a result it can report the probability of an incorrect barcode assignment in SAM auxiliary tags for downstream analysis consideration. It can be used as a drop in substitute for the ubiquitous minimum distance decoding, increasing both precision and recall as well as noise filtering, without hindering speed or memory requirements.
When output is SAM encoded Pheniqs will write the decoding error probability to the XB auxiliary tag for a sample barcode, the XM tag for a molecular barcode and the XC tag for a cellular barcode. In the case of a decoding failure no error probability is reported.
Decoding overview
PAMLD identifies a barcode from a list of potential barcode sequences by maximizing the posterior probability that the selected barcode was sequenced given the potentially erroneous sequence was reported by the instrument. The posterior probability is evaluated using a Bayesian equation that takes into account the conditional decoding probabilities for each potential nucleotide sequence, computed directly from the basecalling quality scores, and a set of prior probabilities. The prior probabilities, the expected fraction of reads identified by each barcode in the data as well as the fraction of indeterminate sequences (random noise), are either provided by the user using the concentration and noise configuration attributes or estimated from the data by a preliminary Pheniqs run that produces a prior adjusted configuration file.
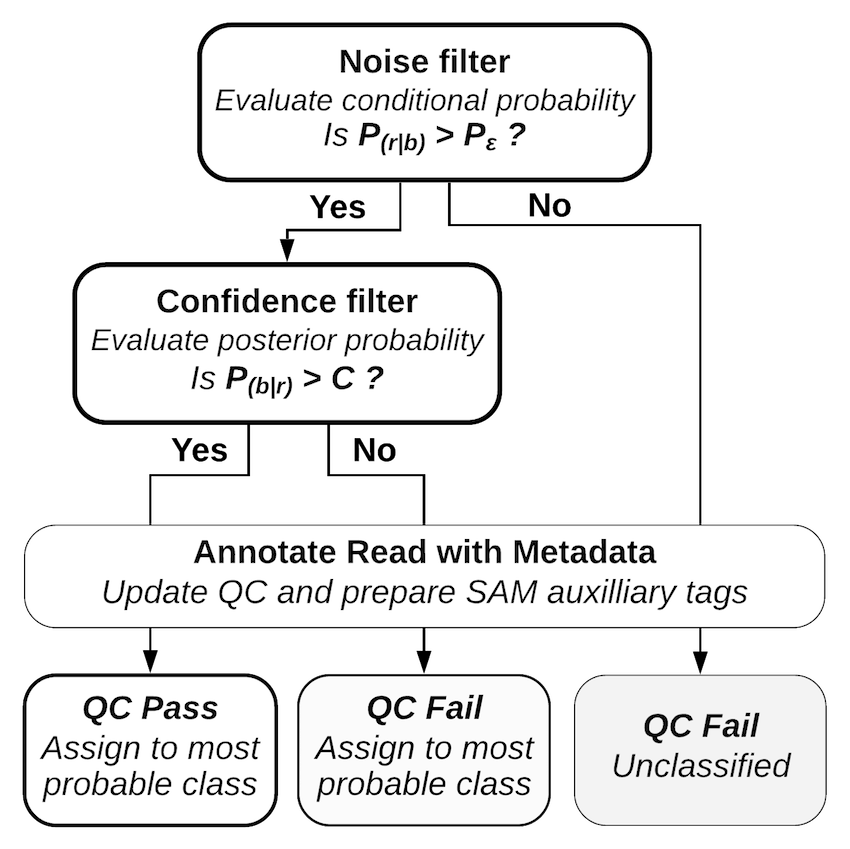
Decoding a read with PAMLD Reads with a lower conditional probability than random sequences fail the noise filter and are classified as noise without further consideration. Reads with a posterior probability that does not meet the confidence threshold fail the confidence filter; these reads are classified, but they are marked as “qc fail” so the confidence threshold can be reconsidered at alater stage. A full description of the mathematics behind Pheniqs, as well as performance evaluations and comparisons with other decoding methods, may be found in the paper. Pheniqs is designed to accommodate the addition of alternative decoders, which can be added as derived classes of a generic decoder object.
Decoding parameters
The dominant user configurable parameter is the confidence threshold, which is a lower bound on the decoding probability to declare a successful classification. The value of confidence threshold controls the tradeoff between false positives and false negatives. Barcode frequencies are specified in the class concentration attribute while the expected decoding failure frequency is specified in the decoder noise attribute.
Another PAMLD parameter influencing noise filtering is the random barcode probability, the probability of observing a particular indeterminate sequence. In the absence of any prior information about potential sequence composition (base distribution or GC bias), we can only assume indeterminate sequences occur with maximum entropy which gives rise to the default value of 1 over 4 to the power of of the length of the barcode. Realistically, however, not every sequence is chemically stable enough to appear in sequencing, indeterminate entropy is lower, and random barcode probability should be set to a higher value determined by empirical studies. Pheniqs accommodates such refinements to the noise model by allowing advanced users to manually set random barcode probability.
Noise filtering
When the conditional probability is lower than random barcode probability, the initial evidence supporting the classification is inferior to that provided by a random sequence, indicating that the maximum likelihood decoded barcode cannot be distinguished from noise. The noise filter considers those a decoding failure without further consideration, and the decoder subsequently sets the QC fail flag for the read.
Reads that pass the noise filter are evaluated by the confidence filter, which verifies that the posterior probability of the maximum likelihood decoded barcode is greater than confidence threshold. If the read passes the confidence filter the probability of a decoding error is given by 1 minus the posterior and reported in the appropriate SAM auxiliary tag, otherwise the QC fail flag is set. In the case of multiple combinatorial barcodes the error probability being reported is 1 minus the product of all individual barcodes of that type, since they are considered to be independent observations.
Directly estimating the posterior decoding probability allows Pheniqs to report intuitive classification confidence scores for every read. Deriving a confidence score for a combinatorial barcode, made up of several independent components, requires to simply multiply the confidence scores of the individual components. confidence threshold allows researchers to choose between assignment confidence and yield of classified reads.
filtering high quality mismatches
Occasionally it might be desirable to filter when a mismatch occurs on a nucleotide with high basecalling quality. For instance when the barcode being decoded is actually a protein coding sequence. A high quality mismatch likely means that the protein is non functional and thus not interesting for further analysis. PAMLD, by nature, penalized high quality mismatches more than low quality ones since it hurts the posterior probability more and so the match is more likely to not clear the confidence threshold. But if you wish to explicitly address such a condition you may specify in the decoder the parameters high quality distance threshold and high quality threshold. If a high quality distance threshold or more number of mismatches are observed in nucleotides with quality high quality threshold or more, the QC fail flag will be set to true. high quality threshold defaults to 30, and high quality distance threshold defaults to 0, which disables the filter.
Estimating the prior distribution
Every Pheniqs decoding run produces, in addition to the output, a JSON encoded statistical report. Statistics from a preliminary PAMLD decoding run can be used to estimate concentration and noise from the data. The high confidence estimator bundled with Pheniqs estimates the relative proportions from the high confidence reads alone, assuming that low confidence reads (those that passed the noise filter but failed the confidence filter) and high confidence reads (those that passed both filters) come from the same distribution.
low conditional confidence count counts reads that failed the noise filter. Those reads are more likely to be noise than anything else. confident noise ratio, computed as low conditional confidence count / ( low conditional confidence count + pf classified count), is a good initial candidate for the noise ratio. This estimation, however, does not account for low confidence reads. When sequencing quality is low the lower signal to noise ratio makes it more difficult to tell random sequences from errors. To correct for this we assume that a noise read is equally likely to be sequenced with low quality and so the same ratio applies to low confidence reads. So an estimate for the total number of noise reads is low conditional confidence count + (low confidence count * confident noise ratio), and the estimate for the noise, is computed by dividing by the total count.
Once noise has been estimated, estimating the prior of each barcode is straight forward since we can rely on the high quality reads. For each barcode the estimated concentration is pf pooled classified fraction multiplied by the probability of it not being noise, which is 1 - noise.
Combinatorial barcodes
When estimating priors for complex combinatorial barcode sets there are multiple strategies available. Pheniqs can decode all barcoding rounds in a single run, in which case the priors will be estimated in an unconditional fashion: every round will be estimated without accounting for the other rounds. This is the quickest but also least accurate estimation.
A different approach is to decode the first round and split the reads to separate files. The prior for the next barcoding round can then be estimated on each of those separate files and so conditional on the previous round. This approach requires multiple decoding rounds but estimating the conditional prior, essentially computing the Bayesian tree, provides more accurate results. The configuration inheritance mechanism makes this easier to script as shown in the fluidigm example.